Excel Least Squares
Excel Least Squares
Files needed: excel_rietveld_01.xlsx
Learning Outcomes: Least squares lies at the heart of most Rietveld refinement packages. In this tutorial we will explore some powder diffraction related aspects of least squares using excel. We’ll build from fitting a simple straight line function to a “full” Rietveld in a later tutorial. If you’re a topas user, you can compare the excel results to equivalent refinements in topas. The excel file above contains several sheets; the ones needed for this tutorial are numbered 4.* and 5.*.
This tutorial has been published in the Journal of Chemical Education. Read more detail here.
1. Save the file listed above in your working directory.
2. Open the excel file excel_rietveld_01.xlsx. Go to the worksheet “solver_linear_fit” which contains the example data used in the lecture.
3. Plot a graph of x and y and use “chart/add trendline” to fit a straight line to the data.
4. Set up columns “ycalc”, “yobs-ycalc” and “(yobs-ycalc)^2” to fit a function y=mx+c to the data. Use solver to minimise the sum of (yobs-ycalc)^2. Plot observed, calculated and difference functions on your graph. Make a note of your results for m and c as we’ll compare them to fitting using topas academic later.
4.5 You may find that solver is not available first time you launch excel. If it doesn’t appear then in office 2010:
Go to File < Options < Add-ins
Click “Go” at the bottom of the screen.
Tick the solver function and click OK.
Solver then appears in the Data tab at the top, on the far right.
5. Try modifiying your calculated function in excel to a quadratic y = ax^2+c.
6. You might want to try an equivalent fit using topas academic at this point. Go to the tutorial here to try this.
7. Sheet “solver_fit_gaussian” contains a data set with a single peak. This could represent a peak in a powder diffraction pattern. Try fitting a simple Gaussian function to this peak. Young (‘Table 1.2) gives a Gaussian function as:
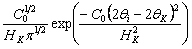
Where:
C0 is 4*ln(2)=2.773
HK is the full width at half maximim.
2theta(i) is the 2theta value and 2theta(K) is the peak position
In excel set up columns of “ycalc”, “yobs-ycalc” and “(yobs-ycalc)^2” and try to fit the experimental data.
8. What other function do you need to complete your fit?
9. Go to sheet fit_gaussian_answer which gives one “model answer” to the problem above. In this and later sheets quantities you can refine are shaded in yellow. (yobs-ycalc)^2 which you can minimise is coloured in light blue.
10. Change the intensity of the reflection to 50. Then use solver to fit the function by changing position, intensity and fwhm of the peak. Before you run solver go into the “options” box and tick “show iteration results” so you can see the pathway that minimisation takes. You need to click “continue” (or hit return) after each cycle of least squares.
11. Now change the starting peak position to 2.5 and try to use solver to fit the data. It should converge easily.
12. Now change the starting values to (pos, int, fwhm = 2.0, 200, 0.3) and try to fit the data. Does the refinement converge to a sensible minimum? If the answer doesn’t look sensible select “restore original values” in excel.
13. What is the smallest value for the peak position where you can get convergence. What’s the critical thing that seems to control whether you get convergence?
14. If you start the peak position at 1.0 what can you do to the other variables to get the refinement to converge?
15. What does this tell you about Rietveld refinement?
16. Gaussian peak shapes are sometimes encountered with low resolution neutron powder diffractometers. The peak shapes in most powder diffraction data is a combination of effects due to the instrument and the sample (see later peak shape tutorials on convolution). Laboratory X-ray data often has a peak shape that is better described by a Lorentzian function or a pseudo-Voigt function (a mixture of Lorentzian and Gaussian shapes). Young gives the equation of a Lorentzian as:
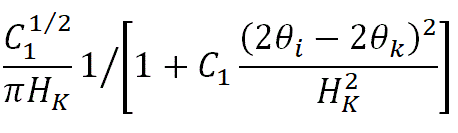
Where HK is the peak fwhm and C1 is 4. |f you are using John’s layout of spreadsheet the excel equation is:
L=$C$16*$B$4^0.5/($B$5*$D$16*(1+($B$4/$D$16^2)*(E2-$B$16)^2))
Try using this function to fit the peak in this example. What do you notice about the shape of a Lorentzian function of intensity 500 compared to a Gaussian with the same intensity? Which function would you choose for an experimental peakshape with large “tails”?
17. Lab x-ray diffractometers typically have pseudo-Voigt peak shapes. You can try fitting a PV in spreadsheet fit_pv_answer. This example uses a single peak from a simulated powder diffraction pattern of TiO2 that you use in later tutorials. What value do you get for the mixing parameter eta?
17. If you’re a topas user, you can compare your Gaussian fitting in excel with an equivalent fitting process in topas. This is detailed in the tutorial linked here.
18. The excel file is linked here.
